TechTool
» Statics 22
» Statics 21
» Statics 20
» Statics 19
» Statics 18
» Statics 17
» Statics 16
» Statics 15
» Statics 14
» Statics 13
» Statics 12
» Statics 11
» Statics 10
» Statics 9
» Statics 8
» Statics 7
» Statics 6
» Statics 5
» Statics 4
» Statics 3
» Statics 2
» Statics 1
The World of Statistics and Probability (1)
By Dr. Magdi Abadir, PhD
Article 21: An introduction to Probabilities (7)
6. Independent events
Two events A and B are said to be independent if the occurrence of any of them does not depend on that of the other.For example, if two people living in two different cities pass driving license exams, the success of the first doesn’t affect the success of the second and vice versa. These two events are therefore independent. On the other hand, if one of these people is a bad driver (A), then this will affect his chances of getting his license (L). In that case, A and L are not independent.
If A and B are independent events, then the probability of both events occurring together is the product of their individual probabilities:
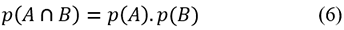
For example, if the probability that A obtains his license is 0.84 and that of B obtaining his is 0.68, then the probability that both will obtain their licenses = 0.84×0.68=0.5712.
The same concept applies for the number of choices: If two independent events A and B can take place in N(A) and N(B) ways respectively, then the number of possibilities of both occurring together is N(A)×N(B).
(7)
7. Probabilities involving permutations or combinations
In my last two articles (#19 and 20), I presented the basics of counting methods, including the use of permutations and combinations. The present section will review the use of this principle in the calculation of probabilities by applying the rules of probabilities (1 to 7) to two of the three examples discussed in the previous article.7.1 The choice of a committee
A 4 – members committee is to be chosen from 10 employees
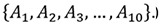We now use the very definition of probability to determine the following:* What is the probability that
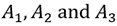are among the chosen 4 persons?
The basic definition of probability of an event A is: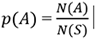 
N(S) is the total number of choices =
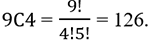
N(A) is the number of choices of the event considered. Here we have to choose three particular persons
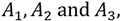while the fourth will be chosen among the remaining 7 persons in 7C1=7 ways. There is only one way to choose the three particular persons, while there will be 7 ways to choose the remaining one. Hence, from rule (7):
N(A)=1×7=7. Therefore, the required probability =
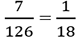
* What is the probability that
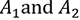are among the chosen 4 persons?
Here, N(S)=126. To obtain N(A), we consider the fact that there is only one choice for choosing
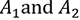, while the other 2 will be chosen among the 8 remaining persons in 8C2=28 ways. Hence, according to rule (7): N(A)=1×28=28
Therefore, the required probability =
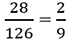
* What is the probability that either
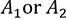are chosen?
N(S)=126, as in the previous cases. Since the required probability involves an (or) event, the following rule is applied (Rule 4 – refer to article 18):
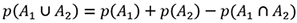
We consider three possible choices:
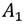is chosen and 
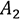is not. 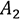is chosen and 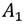is not. 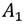and 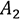are both chosen.
So, there is one choice for A_1 and 8C2=28 ways for the remaining 8 (A_2 is not included in the remaining choices). Hence:
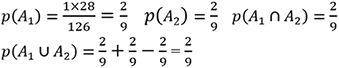
7.2 The parking problem
We recall that in a parking lot containing 8 slots, there were 126 ways for 4 different cars to park side by side.
To calculate the probability that the 4 cars would park side by side, an event we denote by A, we need first to determine N(S), the number of ways the 4 cars can be distributed randomly on the 8 slots. Since the cars are not identical, then the order in which they park must be taken into consideration. This means that this is a case of permutation rather than combination, and N(S)=8P4=8×7×6×5=1680.
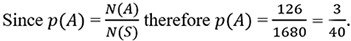
References
(1) https://flexbooks.ck12.org/
cbook/ck-12-conceptos-de-%C3%A1lgebra
-nivel-b%C3%A1sico-en-espa%C3%B1ol/
section/7.9/related/lesson/
probability-and-combinations-bsc-alg/
| Dr. Magdi Fouad Abadir,Ph. D.: Dr. M. F. Abadir is currently a professor with the Chemical Engineering Department at the Faculty of Engineering, University of Cairo, Egypt. His major interests are in the fields of high temperature science and technology. During his career, he has supervised more than 110 MSc and PhD theses and published more than a hundred papers mostly in international peer review journals. He currently teaches courses in High Temperature Technology and Industrial Statistics. He is also a consultant for several industrial businesses. |
