"Optimanage.com"

The World of Statistics and Probability

By Dr. Magdi Abadir, PhD

Article 16: An introduction to Probabilities - 2

2.3 Venn diagrams and some terminologies ⁽¹⁾

Venn diagrams are pictorial representation of sets from which it is possible to establish some simple definitions and subsequent rules.

Consider the set S of all positive integers from 1 to 10 and the two sets: A={1 ,2 ,3 ,4 ,5} and B={2 ,4 ,6 ,7}. These can be represented by the diagram shown in Figure 1. In the present case, S is called a universe as it represents the whole entity of numbers involved in the example.

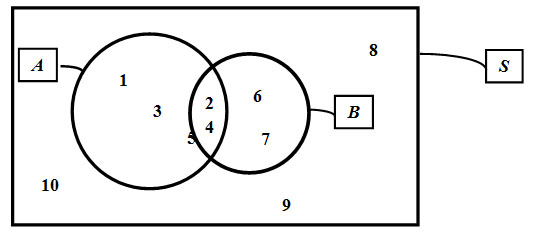
Fig 1: Venn diagram

The set of elements that are not present in A is called the complementary set of A and takes the symbol A^'={6 ,7 ,8 ,9 ,10}. Likewise B^'={1 ,3 ,5 ,8 ,9 ,10}. The set of elements common to A and B is called their intersection and takes the symbol A∩B={2 ,4}.

The set of elements present in either A or B is called their union and takes the symbol A∪B={1 ,2 ,3 ,4 ,5 ,6 ,7}.

The set of elements present in A but not in B is called a difference and takes the symbol A-B={1 ,3 ,5}. Likewise, B-A={6 ,7}.

Based on the previous definitions, one can deduce the following simple rules:

S' = ∅: That is, the complementary of the universe is an empty set.

A∩A'= ∅ and A∪A' = S

A∩∅ = ∅ and A∪∅ = A

A∩S = A and A∪S = S

(A∩B)' = A'∪B'. Here, both are equal to {1 ,3 ,5 ,6 ,7 ,8 ,9 ,10}

(A∪B)' = A'∩B'. Here, both are equal to {8 ,9 ,10}. In the Venn diagram, this is represented by the set of numbers out of the union zone.

If no elements are common between two sets A and B, then they will show on the Venn

diagram without
(Figure 2) and

any intersection
A∩B=∅

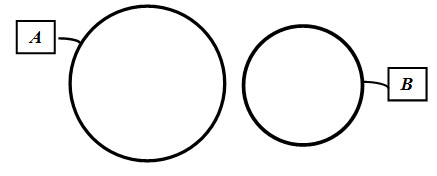
Fig 2: Two sets without any common elements
Finally, if A is a subset of B (A⊂B), then:
A∩B = A and A∪B = B (Figure 3)

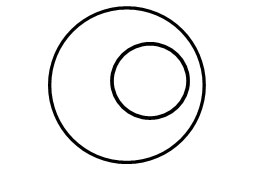
Fig 3: A is a subset of B

Reference:
(1) H. B. Enderton “Elements of set theory” Academic Press., Chapter 1 (1977)

Dr. Magdi Fouad Abadir, Ph. D.: Dr. M. F. Abadir is currently a professor with the Chemical Engineering Department at the Faculty of Engineering, University of Cairo, Egypt. His major interests are in the fields of high temperature science and technology. During his career, he has supervised more than 110 MSc and PhD theses and published more than a hundred papers mostly in international peer review journals. He currently teaches courses in High Temperature Technology and Industrial Statistics. He is also a consultant for several industrial businesses.

HOME		ABOUT US
VIEWPOINT		FOOD FOR THOUGHT
TECHTOOL		MANAGERIA
INFO MIX		ADEL J HELOU COACHING

TechTool

The World of Statistics and Probability

By Dr. Magdi Abadir, PhD

Article 16: An introduction to Probabilities - 2

2.3 Venn diagrams and some terminologies ⁽¹⁾

Site Map

"optimanage.com" TERMS & CONDITIONS

TechTool

The World of Statistics and Probability

By Dr. Magdi Abadir, PhD

Article 16: An introduction to Probabilities - 2

2.3 Venn diagrams and some terminologies (1)

Site Map

"optimanage.com" TERMS & CONDITIONS

2.3 Venn diagrams and some terminologies ⁽¹⁾