TechTool
» Statics 22
» Statics 21
» Statics 20
» Statics 19
» Statics 18
» Statics 17
» Statics 16
» Statics 15
» Statics 14
» Statics 13
» Statics 12
» Statics 11
» Statics 10
» Statics 9
» Statics 8
» Statics 7
» Statics 6
» Statics 5
» Statics 4
» Statics 3
» Statics 2
» Statics 1
The World of Statistics and Probability (1)
By Dr. Magdi Abadir, PhD
Article 19: An introduction to Probabilities (5)
1.The basic principle of counting
Consider that a boy Bill must choose a snack composed of a sandwich and a Juice. There are 3 types of sandwiches {A,B,C} and two types of juice {D,E}. He will have the following choices:• He chooses sandwich A and juice D.
• He chooses sandwich A and juice E.
• He chooses sandwich B and juice D.
• He chooses sandwich B and juice E.
• He chooses sandwich C and juice D.
• He chooses sandwich C and juice E.
The number of possible choices (6) is simply obtained by multiplying the number of choices from the sandwich selection (3) by the number of choices from juice types (2). This simple rule is known as the principle of counting. In general, it states that if we are in presence of a series of different items whose numbers are
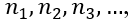then the number of possible ways to choose one item of each series will be: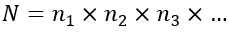
For example, if a director in a firm decides to randomly choose one representative of the technical department, which contains 16 employees, and a second from the financial department, containing 24 employees and a third from the legal department, containing 12 employees, so he will have a rather large choice of 16×24×12=4608 ways!
2. Permutations
Consider a boy who chooses two balls out of a bag containing 10 balls numbered from 1 to 10 so that he doesn’t replace the ball chosen in the first draw. He has 10 choices for the first draw and 9 for the second since the chosen ball in the first draw was not replaced. Following the counting principle, there are 10×9=90 ways to carry out these choices.If a third draw is carried out without replacement, then the number of outcomes = 10×9×8=720 etc. This product is called a permutation and is written as follows: 10P3=10×9×8.
If the trials are repeated without replacement, then, ultimately, we will be left with one ball only. In that case the number of outcomes = 10×9×8×…×3×2×1=10P10. It is customary to denote the permutation term
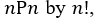and it is called the 
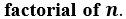The permutation term 
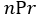can be written in for of factorials as follows:
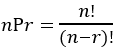
(7)
3. Combinations
If the boy decides to garb three balls at a time in one draw, then the number of ways of carrying out this operation is called a combination, and the number of possible outcomes is written 10C3. This is calculated by the following rule: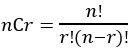
(8)
For example, the number of ways to choose three balls out of a bag containing 10 distinct
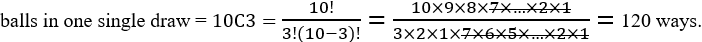
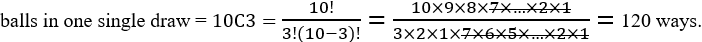
4. Types of choice
Choosing 2 balls out of 10 placed in a bag can be accomplished in three ways:4.1 Choice with order and replication
If we choose one ball, replace it in the bag, then choose a second, then there will be 10 possible outcomes each time, and according to the counting principle, the number of choices will be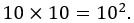
In general, if we choose one object at a time from n different objects and replace it each time, then, the number of possible ways of repeating this operation
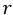times will be: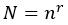
(9)
4.2 Choice with order without replication
In that case, as previously explained in section 2, the total number of choices will be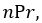
which can be calculated from Equation (7).4.3 Choice without order and without replication
This is the case of choosing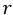 objects out of 
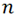at a time. In that case, as previously explained in section 3, the total number of choices will be 
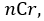which can be calculated from Equation (7).For example, choosing 3 numbers out of 9 can be performed in three ways:
• Choice with order and replication:
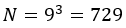
• Choice with order without replication:
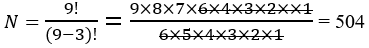
• Choice without order and without replication:
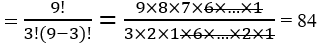
Reference:
(1) https://www.mathplanet.com/education/pre-algebra/probability-and-statistics/combinations-and-permutation
| Dr. Magdi Fouad Abadir, Ph. D.: Dr. M. F. Abadir is currently a professor with the Chemical Engineering Department at the Faculty of Engineering, University of Cairo, Egypt. His major interests are in the fields of high temperature science and technology. During his career, he has supervised more than 110 MSc and PhD theses and published more than a hundred papers mostly in international peer review journals. He currently teaches courses in High Temperature Technology and Industrial Statistics. He is also a consultant for several industrial businesses. |
