TechTool
» Statics 22
» Statics 21
» Statics 20
» Statics 19
» Statics 18
» Statics 17
» Statics 16
» Statics 15
» Statics 14
» Statics 13
» Statics 12
» Statics 11
» Statics 10
» Statics 9
» Statics 8
» Statics 7
» Statics 6
» Statics 5
» Statics 4
» Statics 3
» Statics 2
» Statics 1

The World of Statistics (1)
By Dr. Magdi Abadir, PhD
Article – 14: Measures of Dispersion (4)
2.4 The standard deviation and coefficient of variation of grouped data
In case of grouped data, the determination of the standard deviation and subsequently the coefficient of variation is slightly different. First, it is necessary to differentiate between whether we intend to investigate dispersion in a population or in a sample. This is since two different formulas are used in each case.Standard deviation of a population
Let us assume that a megastore sells items in different price categories. In that case we are dealing with a population where the number of items in each category will follow a certain distribution as in the following table:In case of population, the standard deviation is calculated from the formula:
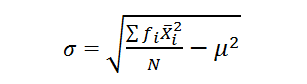
Here, ƒɩ represents the total number of items in class (ɩ), x̄ɩ the mean value of class (ɩ), N the total number of items(∑ƒɩ) and μ the average selling price defined by:
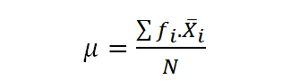
The calculations are illustrated in the following table:
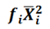
|
| Therefore | 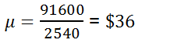 |
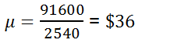
| Therefore, | 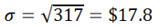 |
| The coefficient of variation |  |
Standard deviation of a sample
Let’s assume now that an instructor chooses at random 50 students from a large graduating cohort and sets to estimate the standard deviation of their scores in their graduation project (out of 50). Now we are in presence of a sample of size 50. Let the distribution be as follows:The formula for the standard deviation takes the form:
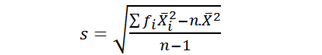
The following table shows the calculations
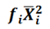
|
| Therefore, | 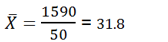 |
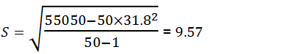
| The coefficient of variation | 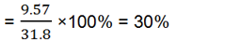 |
References:
(1) W. J. De Coursey “Statistics and Probability for Engineering Applications” Newness Ed., Chapter 3.
| Dr. Magdi Fouad Abadir, Ph. D.: Dr. M. F. Abadir is currently a professor with the Chemical Engineering Department at the Faculty of Engineering, University of Cairo, Egypt. His major interests are in the fields of high temperature science and technology. During his career, he has supervised more than 110 MSc and PhD theses and published more than a hundred papers mostly in international peer review journals. He currently teaches courses in High Temperature Technology and Industrial Statistics. He is also a consultant for several industrial businesses. |




