TechTool
» Statics 22
» Statics 21
» Statics 20
» Statics 19
» Statics 18
» Statics 17
» Statics 16
» Statics 15
» Statics 14
» Statics 13
» Statics 12
» Statics 11
» Statics 10
» Statics 9
» Statics 8
» Statics 7
» Statics 6
» Statics 5
» Statics 4
» Statics 3
» Statics 2
» Statics 1

The World of Statistics and Probability (1)
By Dr. Magdi Abadir, PhD
Article 18: An introduction to Probabilities (4)
4. Some basic rules of probabilities
Besides the two criteria for probability functions, enunciated at the end of the last article (17), there are some basic rules, which are essential for a more profound understanding of probabilities principles. Some of them can be understood intuitively, while others will be given without proof.4.1 The probability of a complementary event
Let A be an event and A’ its complementary, then:
p(A^' )=1-p(A)
(1)
Such a result is obvious, for, if the probability that it will rain today is 0.7 (or 70%), then the probability that it will not rain will be 1-0.7=0.3 (30%).
4.2 The probability of space and empty set
Since the space S comprises all possible events, then its probability is simply 100%:
p(S)=1
(2)
On the other hand, the empty set ∅ , being complementary to S, its probability is nil, as per equation (1):
p(∅)=0
(3)
For example, if we choose a number from 1 to 10, then the probability that the chosen number will be greater than 0 is 1, while the probability that the number 12 will be chosen is zero.
Since the probability of sample space S is 100%, it is often referred to as “Certain event”, while the impossible occurrence of the empty set has prompted calling it “Impossible event”.
4.3 The probability of the union of two events
Let A and B be two events ⊂S. The probability that at least one of them will occur is the probability of A∪B. On the other hand, the probability that they will occur simultaneously is that of A∩B. The following rule allows calculating the probability of A∪B.
p(A∪B)=p(A)+p(B)-p(A∩B)
(4)
Let’s have a more detailed look at that last rule:
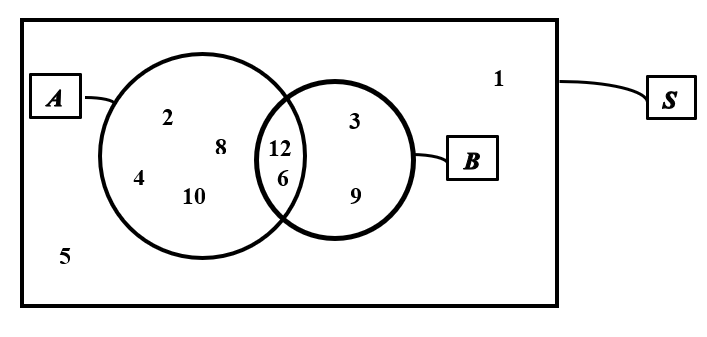
Consider the set of integers from 1 to 12. There are 6 even numbers among in that set: A={2,4,6,8,10,12} while there are 4 numbers divisible by 3: B={3,6,9,12}.
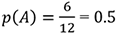
(i)
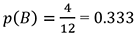
(ii)
The intersection of these two sets represents the numbers that are common to both:
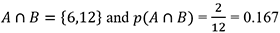
(iii)
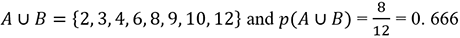
(iv)
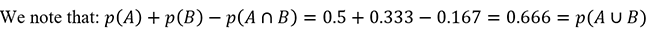
The following Venn diagram helps understanding the concept.
A special case occurs if the two sets have no common elements, which can be expressed as A∩B=∅. In that case, the application of rules (3) and (4) results in the simple result:
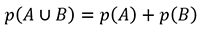
(5)
Reference:
W. Mendenhall, R. J. Beaver and B. M. Beaver “Introduction to Probability and Statistics” 14th Edition. Brooks – Cole, CENGAGE learning. (2013), Chapter 4
| Dr. Magdi Fouad Abadir, Ph. D.: Dr. M. F. Abadir is currently a professor with the Chemical Engineering Department at the Faculty of Engineering, University of Cairo, Egypt. His major interests are in the fields of high temperature science and technology. During his career, he has supervised more than 110 MSc and PhD theses and published more than a hundred papers mostly in international peer review journals. He currently teaches courses in High Temperature Technology and Industrial Statistics. He is also a consultant for several industrial businesses. |



