TechTool
» Statics 22
» Statics 21
» Statics 20
» Statics 19
» Statics 18
» Statics 17
» Statics 16
» Statics 15
» Statics 14
» Statics 13
» Statics 12
» Statics 11
» Statics 10
» Statics 9
» Statics 8
» Statics 7
» Statics 6
» Statics 5
» Statics 4
» Statics 3
» Statics 2
» Statics 1
The World of Statistics and Probability
By Dr. Magdi Abadir, PhD
Article 22: An introduction to Probabilities (8)
8. Conditional probabilities (1)
Consider the following situation:
Four of the light bulbs in a box of ten bulbs are burnt out or otherwise defective. If two bulbs are selected at random, one by one without replacement, and tested. What is the probability that exactly two defective bulbs are found?
The probability that the first chosen bulb will be defective π(π·1) = (4/10).
The probability that the second one will also be defective depends on the first choice: If the first one was defective, then there will be 3 defective bulbs among the remaining 9. This probability is denoted by π(π·2/π·1) and is read: The probability that the second bulb is defective if the first one is defective. This defines conditional probability. In the present case: π(π·2/π·1) = (3/9)
The probability that two defective bulbs chosen one by one without replacement will be found involves the use of permutations (See article 19, equation 7). It equals: π(π·1 β© π·2) = (4π2) / (10π2) = (4Γ3) / (10Γ9) = π(π·1). π(π·2/π·1)
Therefore, conditional probability can be defined as follows: π(π·2/π·1) = π(π·1β©π·2) / π(π·1) β¦β¦β¦β¦β¦. (8)
Situations involving the use of conditional probabilities are best dealt with by using βtree diagramsβ. The previous problem can be pictured as follows (see Figure β 1):
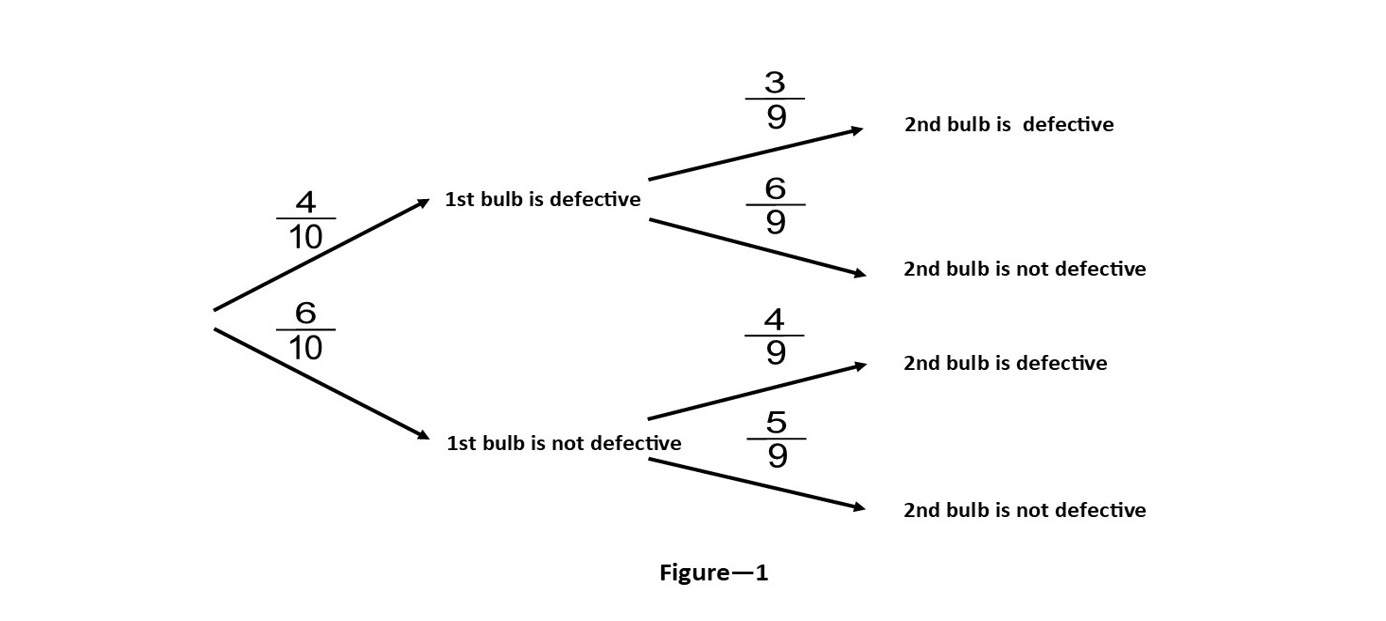
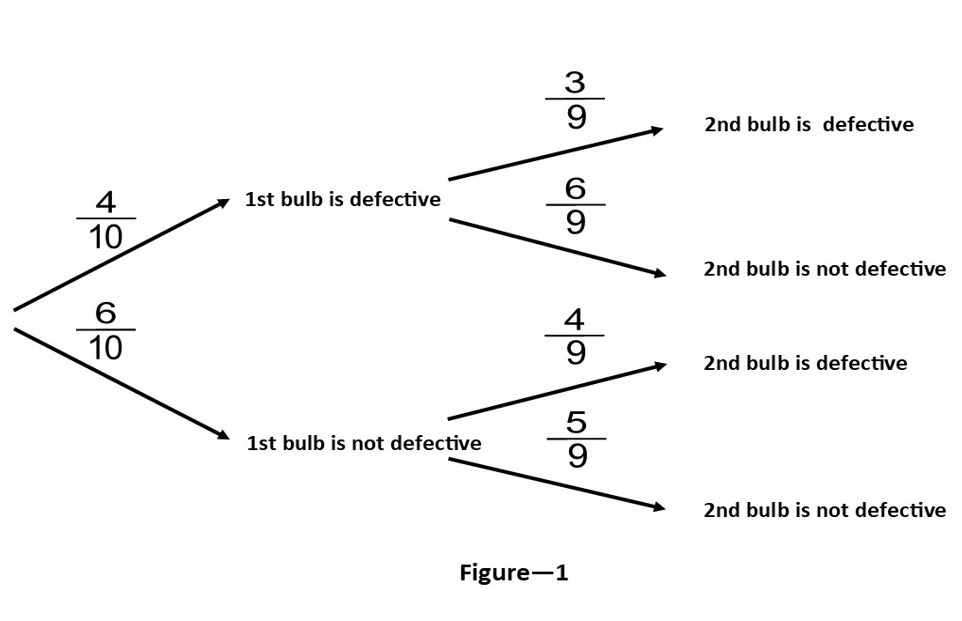
This diagram enables answering any question about all possible outcomes of the two draws. For example, the probability that the first bulb chosen is defective and the second non-defective is obtained by simply multiplying the probabilities on the corresponding arrows, in which case we get:
π(π·β2/π·1) = (4/10) Γ (6/9)
The four possible final outcomes of the two draws will be:
Both bulbs are defective: π(π·1 β© π·2) = (4/10) Γ (3/9) = (12/90)
The first bulb is defective and the second non-defective: π(π·1 β© π·β2) = (4/10) Γ (6/9) = (24/90)
The first bulb is non-defective and the second defective: π(π·β1 β© π·2) = (6/10) Γ (4/9) = (24/90)
Both bulbs are non-defective: π(π·β1 β© π·β2) = (6/10) Γ (5/9) = (30/90)
We note that the total probability of all possible events:
= (12/90) + (24/90) + (24/90) + (30/90) = (90/90) = 1
For example, the probability that the two chosen bulbs will be either defective or non-defective will therefore be: (12/90) + (30/90) = (42/90)
References
(1) W.J. DeCoursey (2003) βStatistics and Probability for Engineering Applicationsβ Ed. Newnes, pages 18 β 19.
| Dr. Magdi Fouad Abadir, Ph. D.: Dr. M. F. Abadir is currently a professor with the Chemical Engineering Department at the Faculty of Engineering, University of Cairo, Egypt. His major interests are in the fields of high temperature science and technology. During his career, he has supervised more than 110 MSc and PhD theses and published more than a hundred papers mostly in international peer review journals. He currently teaches courses in High Temperature Technology and Industrial Statistics. He is also a consultant for several industrial businesses. |
