TechTool
» Statics 22
» Statics 21
» Statics 20
» Statics 19
» Statics 18
» Statics 17
» Statics 16
» Statics 15
» Statics 14
» Statics 13
» Statics 12
» Statics 11
» Statics 10
» Statics 9
» Statics 8
» Statics 7
» Statics 6
» Statics 5
» Statics 4
» Statics 3
» Statics 2
» Statics 1
The World of Statistics and Probability (1)(2)
By Dr. Magdi Abadir, PhD
Article 20: An introduction to Probabilities (6)
5. Some interesting examples
In that article, I will be presenting some interesting examples involving the use of permutations and combinations, before reviewing their use in the calculation of probabilities.5.1 The choice of a committee
A 4 – members committee is to be chosen from 10 employees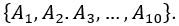 
If the choice is random, then the number of ways of performing all possible choices will be: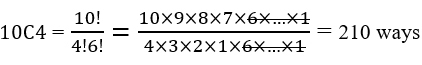
Now, consider the case where a certain employee of poor performance will be discarded from any choice. In that case, one will be choosing the 4 members out of 9 persons only, and the number of choices will be reduced to:
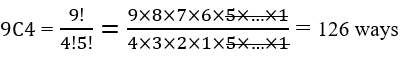
If now one of the employees, having proved exceptional qualities, is to be chosen anyway, then the 3 others will be chosen from the remaining 9 people. The number of choices is:
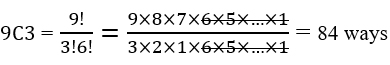
Finally, let there be two people that don’t get along well. Say
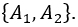It was decided that there was no point having them together in that committee. This way, either 
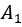only or 
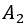only will be chosen or both will be discarded. In the first two events, the choice will be 9C3 and in the third case, 8C4. The total number of possible ways to form the committee will be: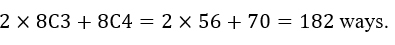 
Another way of solving that last part is to seek the remaining possibility: That both will be chosen, and subtract the number from the total number of possible ways (210):
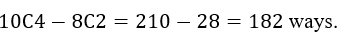
5.2 The distribution problem
In a game involving four pupils, 14 different toys will be distributed among them in the following way: The four names are written on 4 pieces of paper, put in a box, and the papers will be drawn one by one from the box. The first pupil will choose any 5 toys, the second 4, the third 3 and the fourth will be left with the two remaining toys.
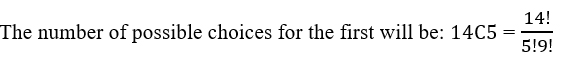
Following the counting principle, the total number of choices will be the product of the four previous combination terms:
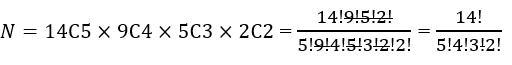
We note that this is the ratio of the factorial of the total number of items, divided by the product of the factorials of the number of consecutively distributed toys. This is an important principle, stating that upon the distribution of
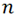items on several sites so that there will be 
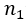items to the first site, 
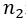items to the second, 
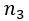items to the third, etc., then the total number of possible ways of carrying out the distribution will be: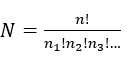
Believe it or not, this principle has applications in quantum physics, in chemistry and several other fields.
5.3 The parking problem
Consider, parking 8 cars in a park so that they are parked in a straight line. The problem I to find by how many ways 4 different cars can park to be side by side.
To solve this problem, we visualize the park as being formed of 48 slots and representing the four cars by a segment line, work out by how many ways can this line fit within the 8 slots. There will be 5 such cases. (See figure).
Each of these 5 cases correspond to the possible permutations of the 4 cars on the 4 slots = 4P4=4!
The total number of ways for the cars to park side by side = 5×4!=120 ways.
References
(1) https://math.stackexchange.com/questions/2763802/find-the-number-of-ways-to-park-cars-next-to-each-other-in-a-parking-area
(2) https://www.chegg.com/homework-help/questions-and-answers/derive-multinomial-coefficient-number-ways-divide-n-objects-three-groups-n1-n2-n3-objects--q18112206
| Dr. Magdi Fouad Abadir,Ph. D.: Dr. M. F. Abadir is currently a professor with the Chemical Engineering Department at the Faculty of Engineering, University of Cairo, Egypt. His major interests are in the fields of high temperature science and technology. During his career, he has supervised more than 110 MSc and PhD theses and published more than a hundred papers mostly in international peer review journals. He currently teaches courses in High Temperature Technology and Industrial Statistics. He is also a consultant for several industrial businesses. |
